[AIB] Confidence Intervals

ANOVA (one-way)

이전에 배운 가설검정방법

→ 1개 그룹의 평균이 특정 값과 같은지 (1-sample t-test)

→ 2개 그룹의 평균이 유의미하게 다른지 (2-sample t-test)

 

ANOVA 가설검정방법은 2개 이상 그룹의 평균에 차이가 있는지를 확인하는 방법이다.

 

Multiple Comparision

2개 이상의 여러 그룹을 비교하기 위해서 여러개를 하나하나씩 비교하는 것은 그룹 수가 늘어날수록 전체 에러도 점점 커지게 된다. 따라서 여러개의 그룹을 한꺼번에 비교하는 방법이 필요하다.

 

Variation

여러 그룹간의 차이가 있는지를 확인하기 위해선 여러 그룹들이 하나의 분포에서부터 왔다 라는 가정을 생각해야 한다.

이를 위한 지표는 F-statistic 이며, F-value가 높다는 것은 어떤 의미를 가질까?

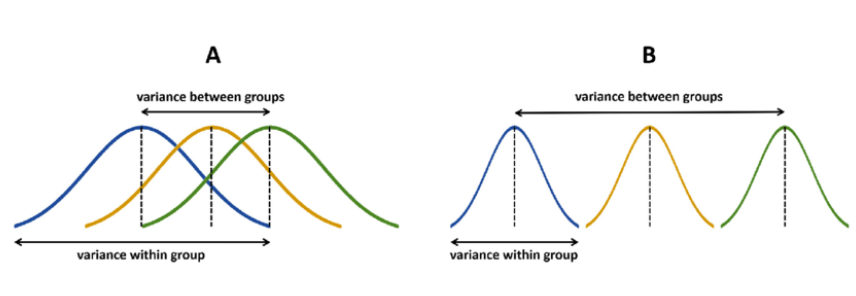
• 분자(다른 그룹끼리의 분산)는 크고, 분모(전체 그룹의 분산)는 작아야 한다.
• 즉 다른 그룹끼리의 분포가 다를 것이다 라는 가정이 붙는다.

 

 

F-stat by scipy

from scipy.stats import f_oneway
import numpy as np

g1 = np.array([0, 31, 6, 26, 40])
g2 = np.array([24, 15, 12, 22, 5])
g3 = np.array([32, 52, 30, 18, 36])
f_oneway(g1, g2, g3)	# pvalue = 0.11

Output :

F_onewayResult(statistic=2.6009238802972483, pvalue=0.11524892355706169)

 

 

Low of large numbers (큰 수의 법칙)

sample 데이터의 수가 커질수록 sample의 통계치는 점점 모집단의 모수와 같아진다.

import numpy as np

population = np.random.normal(50, 10, 1000)	# 평균=50, 표준편차=10, size=1000
population.var()	# 94.676

# sample 5개
np.random.choice(population, 5).var()	# 46.485

# sample 10개
np.random.choice(population, 10).var()	# 106.193

# sample 50개
np.random.choice(population, 50).var()	# 107.840

# sample 100개
np.random.choice(population, 100).var()	# 103.087

 

 

Central Limit Theorem, CLT (중심극한정리)

sample 데이터 수가 많아질수록, sample의 평균은 정규분포에 근사한 형태로 나타난다.

 

 

신뢰 구간의 설정 및 해석

신뢰구간 계산식

from scipy import stats

def confidence_interval(data, confidence=0.95):
	data = np.array(data)
    mean = np.mean(data)
    n = len(data)
    
    # std/sqrt(n) = s/sqrt(n)
    stderr = stats.sem(data)	# standard error of mean
    
    # length_of_one_interval
    interval = stderr * stats.t.ppf( (1+confidence)/2, n-1 )	# ppf(inverse of cdf)
    
    return (mean, mean-interval, mean+interval)

np.random.seed(123)
data2 = np.random.normal(50, 10, 1000)
sample = np.random.choice(data2, 10)
confidence_interval(sample)

Output : (44.28501220284126, 37.93312500671013, 50.63689939897239)

 

reference.

scipy.stats.t.ppf

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.t.html

scipy.stats.t — SciPy v1.7.1 Manual

 

 

CI with scipy

from scipy.stats import t

n = len(sample)	# 표본의 크기
dof = n-1	# 자유도
mean = np.mean(sample)	# 표본의 평균
sample_std = np.std(sample, ddof=1)	# 표본의 표준편차
std_err = sample_std / (n ** 0.5)	# 표준 오차

CI = t.interval(.95, dof, loc=mean, scale=std_err)
print('95% 신뢰구간: ", CI)

Output :

95% 신뢰구간: (37.93312500671013, 50.63689939897239)